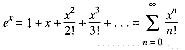
and compares the result to the "correct" answer given by the exp function in the standard library. This works correctly for positive arguments, but the result for negative arguments isn't even close! The problem, of course, is that computers, with their finite capabilities, can only represent a minuscule subset of the set of real numbers. A good chunk of numerical analysis deals with roundoff error, the quirks of finite-precision arithmetic.
In days gone by, many computers used a fixed-point number system, which uses numbers derived from a given radix (b), precision (p), and fraction size (f). For example, the values b=10, p=4, and f=1 define the following set of 19,999 numbers:
F = {-999.9, - 999.8,...,999.8, 999.9}
Since these numbers are evenly spaced, the maximum absolute error in representing any real number x in this system is bounded by 0.05. In other words,
|x-fix(x)| < 0.05The set of machine integers form a fixed-point system with f=0, and a maximum absolute error of 0.5 for systems that round, and no greater than 1.0 for systems that truncate.
Absolute error is not generally useful in mathematical computations, however. As is often the case, you are more often interested in percentages, or how one number differs in relation to another. You compute the relative error of y with respect to x by the following formula:
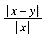
Consider how the numbers 865.54 and 0.86554 are represented in F:
fix(865.54) = 865.5 fix(.86554) = 0.9Because the number of decimals is fixed, the second is a much poorer fit than the first, which the relative errors illustrate:

The second is 1,000 times worse than the first!
Nowadays computers provide floating-point number systems, which represent numbers in the form
±0.d1d2...dp X bewhere
m < e < M, 0 < di < bThis is like the scientific notation that you learned in school, except that in this case the base (b) can be other than 10, and there is an upper limit on the precision (p). Most floating-point systems use a normalized representation, which means that d1 cannot be zero. These number systems are called floating-point for the obvious reason — the radix point "floats" and the exponent (e) adjusts accordingly to preserve the correct value.
Consider a floating-point system G defined by b=10, p=4, m=-2, and M=3. The numbers from the fixed-point example above are represented as:
fl(8.65.54)+0.8655 x 103 fl(865.554)=0.8655 x 100Now look what happens when calculating the relative errors of the two representations:
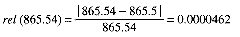
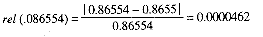
It can be shown that the relative error of representing any real number within the range of a floating-point system is no greater than b1-p, which is 0.001 in G.
Floating-point numbers are not evenly spaced. In G, for example, the next number greater than 1 is 1.001, a spacing of 0.001, but the next number after 10 is 10.01, which is 0.01 to the right. In general, the spacing among all numbers between powers of b, say between be and be+1, is be+1-p. A trivial combinatorial analysis shows that each interval [be, be+1] has (b—1) bp-1 floating-point numbers, and the total number of representable floating-point numbers in a system is 2(M—m+1)(b—1)bp-1 (so increasing p increases the density of the number system). And as shown above, although smaller numbers are closer together and larger numbers are farther apart, the relative spacing between consecutive floating-point numbers is essentially the same throughout the system. In fact, the relative spacing between two adjacent representable numbers within an interval [be, be+1] is b1-p, and between be+1 and its immediate predecessor is b-p.
The quantity b1-p, which also happens to be the spacing between 1.0 and its immediate successor, is called the machine epsilon (e), and is a good measure of the granularity of a floating number system. The smallest floating-point magnitude other than zero is of course b, usually denoted as s, and the largest magnitude, l, is bM(1—b-p).
The Standard C header <float.h> provides manifest constants for all of these parameters as follows:
b == FLT_RADIX p == DBL_MANT_DIG m == DBL_MIN_EXP M == DBL_MAX_EXP e == DBL_EPSILON s == DBL_MIN l == DBL_MAX<float.h> also provides the float and long double equivalents of the last five parameters, representing the three (not necessarily distinct) floating-point number systems in standard C (see Table 4) .
The program in Listing 2 calculates a root of x2+x+1 in the interval [—1, 1] by the method of bisection. The algorithm halves the interval (which must contain a sign change for the function F) until the relative spacing between the endpoints is less than or equal to machine epsilon. Such a loop may never terminate if you expect greater precision than this.
Should you find yourself in an environment that does not provide the parameters in <float.h>, you can compute b, p, and e directly. To see how this is possible, remember that the spacing between consecutive floating-point numbers increases with the magnitude of the numbers. Eventually there is a point where the spacing between adjacent numbers is greater than 1. (In fact, the first interval where this holds true is [bp, bp+1], because the integers therein require p+1 digits in their representation.) The positive integers precisely representable in a floating-point system are these:
1,2,...,bp-1,bp,bp+b,bp+2b,..., bp+1,bp+1+b2,...To find the radix, the program in Listing 3 keeps doubling a until it reaches a point where the spacing exceeds 1. It then finds the next larger floating-point number and subtracts a to get b. The program then computes the smallest power of b that will produce numbers whose adjacent spacing exceeds 1 that power is the precision p. To find e, the program finds the nearest representable neighbor to the right of 1, and subtracts 1.